Bonjour,
Qu'ils soient considérés ou non à réaction équilibrée, cela importe peu, car les résultats pratiques sont indépendants de la considération.
Je pense plus profitable d'orienter mon raisonnement sur les possibilités de mouvement des systèmes d'engrenages similaires.
Je sollicite votre avis au sujet d’un ensemble d’engrenages en schéma, dont je suis incapable d’imaginer avec certitude le comportement réel.
J’ai tenté sans succès, de comprendre la formule de Willis et je n’ai pas la possibilité de réaliser l’expérience.
Je m’adresse à vous qui êtes compétent en mécanique, en espérant que vous pourrez orienter mon raisonnement.
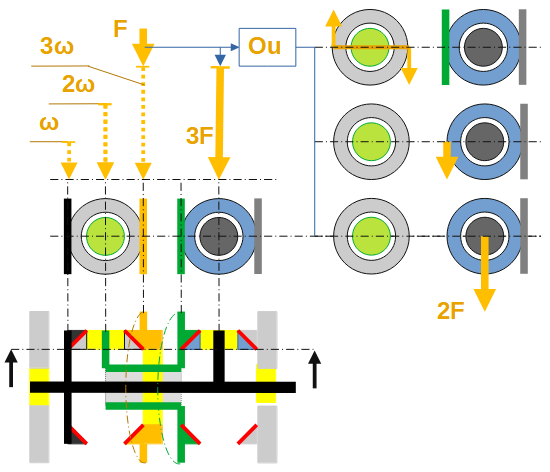
Les pignons coniques gris et bleu sont identiques et libres sur leur axe respectif, vert et noir.
Le pignon conique noir et l’axe noir vertical, sont solidaires de l’axe noir horizontal qui est libre.
Le pignon conique de carcasse est fixe et est identiques aux trois pignons verticaux, noir, orange et vert.
Le pignon conique orange est libre sur l’axe creux horizontal vert.
Le pignon conique vert et l’axe vertical vert, sont solidaire de l’axe creux vert horizontal.
Toutes les distances d’action d’éventuelles forces aux axes verticaux sont égales.
Toutes les distances d’action d’éventuelles forces aux axes horizontaux sont égales.
J’ai appris que :
Sans considération des pertes, les systèmes d’engrenages transmettent toujours l’intégralité des forces et puissances qu’ils reçoivent.
Voici mon dilemme :
1) Soit : F en rotation à 3ω devrait se reporter sur l’axe noir vertical d’une valeur de 3F à ω.
2) Soit : F se remplace par un couple de force F/2 sur le pignon gris. L’action de se couple sur l’axe vertical vert, est alors une force F, ainsi que sur le pignon conique vert, action qui applique une force égale à 2F sur l’axe vertical noir.
3) Soit : Il existe un autre raisonnement que je n’ai pas réussi à élaborer.
Merci d’avance pour vos réponses.
L’objectif de ce système d’engrenages, est d’obtenir l’équilibre de l’ensemble avec une force égale et opposée à F sur le pignon conique vert. Cela ne serait possible que dans le cas 2.